We explain what an axiom is in logical thinking, philosophy and mathematics. Also, examples of famous axioms.
What is an axiom?
In the world of knowledge and knowledge, it is known as an axiom any proposition or premise that is considered self-evidentthat is, obvious, easily demonstrable, and which serves as the foundation for a body of theories and deductive reasoning.
The axioms They are general and basic rules of logical thinkingwhich exist in countless disciplines, scientific or not, and which are distinguished from postulates by the fact that they do not require a demonstration (as they are evident) and therefore must simply be accepted. It is possible to compare them with a seed: in them is condensed what is necessary for an entire theoretical tree of thought to sprout.
The word axiom comes from the Greek axiom (“authority”), in turn derived from the noun axios (“meritorious” or “adequate”), as already used by the classical philosopher Aristotle (384-322 BC): “everything that is assumed to be the basis of a demonstration, a principle in itself evident.”
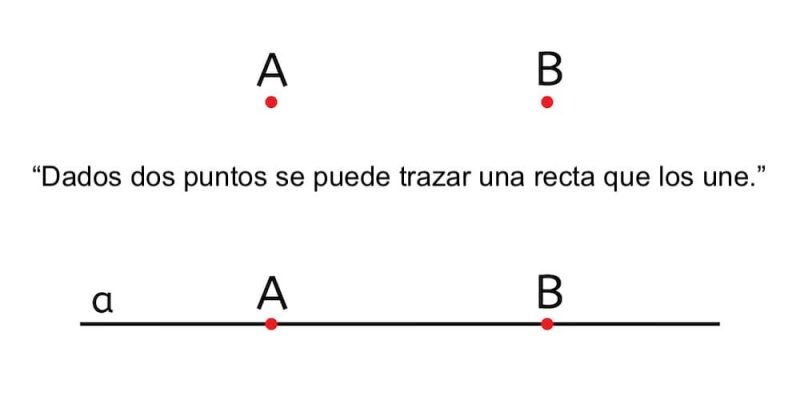
In fact, it was the great Greek mathematicians who bequeathed to history a very small set of simple axioms, obtained after the logical reduction of various theorems and mathematical problems.
Axioms are very common in formal disciplines, such as logic or mathematics.but it is also possible to find them in very different disciplines, although the term is often used in a metaphorical sense, to say that an idea is fundamental or indispensable.
Examples of axiom
Some examples of axioms are the following:
- Euclid's elementsformulated by this Greek mathematician and geometer (ca. 325-265 BC) in the 4th century BC. C., are made up of a set of “common notions”, which we can perfectly qualify as axioms.
- The axiom of choiceformulated in 1904 by the German mathematician Ernst Zermelo (1871-1953), establishes that every set can be well ordered, that is, for each family of non-empty sets that exists, there is also another set that contains one element of each. of yours.
- The axioms of human communicationformulated by the Austrian theorist Paul Watzlawick (1921-2007), establish the five fundamental and self-evident principles according to which all forms of communication between human beings occur.
Continue with: Formal sciences
References
- “Axiom” on Wikipedia.
- “Axiom” in the Language Dictionary of the Royal Spanish Academy.
- “Axiom” in the Online Spanish Etymological Dictionary.
- “Axiom” in the Herder Encyclopedia.
- “Axiom” in The Encyclopaedia Britannica.





